eo_logo
 

 
Focal Length Calculator

View All Technical Tools

OR Plano 

OR Plano 

  

Effective Focal Length, EFL (mm): --       

Back Focal Length, BFL (mm): --       

Front Focal Length, FFL (mm): --       

Primary Principal Point, P (mm): --       

Secondary Principal Point, P'' (mm): --       

Shift in Nodal Point (mm): >--       

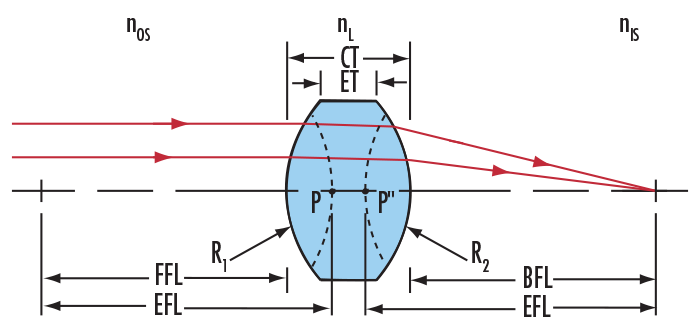
Focal Length Calculator
$$ \Phi_{\text{OS}} = \frac{n_L - n_{\text{OS}}}{R_1} $$
$$ \Phi_{\text{IS}} = \frac{ n_{\text{IS}} - n_{L} }{R_2} $$
$$ \Phi = \Phi_{\text{OS}} + \Phi_{\text{IS}} - \Phi_{\text{OS}} \, \Phi_{\text{IS}} \, \left( \frac{\text{CT}}{n_L} \right) $$
$$ P'' = - \frac{\Phi_{\text{OS}}}{\Phi} \, \left( \frac{n_{\text{IS}}}{n_L} \right) \, \text{CT} $$
$$ \text{EFL} = \frac{1}{\Phi} $$
$$ f_F = - n_{\text{OS}} \cdot \text{EFL} $$
$$ f_R = n_{\text{IS}} \cdot \text{EFL} $$
$$ \text{BFL} = f_R + P'' $$
$$ \text{FFL} = f_F + P $$
$$ \text{NPS} = f_F + f_R $$
$$ P = \frac{\Phi_{\text{IS}}}{\Phi} \, \left( \frac{n_{\text{OS}}}{n_L} \right) \, \text{CT} $$
ΦOS Power of Surface 1
ΦIS Power of Surface 2
F Lens Power
nOS Object Space Index
nL Lens Index
nIS Image Space Index
R1 Radius of Surface 1
R2 Radius of Surface 2
CT Center Thickness
P Primary Principle Point
P" Secondary Principle Point
EFL Effective Focal Length
BFL Back Focal Length
FFL Front Focal Length
NPS Nodal Point Shift
fF Front Focal Point
fR Rear Focal Point

Note: This calculator follows the standard sign convention for the optical radius of curvature where if the vertex of a surface lies to the left of the center of curvature the radius of curvature is positive, and if the vertex lies to the right of the center of curvature the radius of curvature is negative. In the figure, R1 is positive and R2 is negative.

Description

Relate optical and mechanical parameters of simple lenses in order to ease integration into application assemblies. Select index from list of EO's own optical substrates to help calculate focal lengths and principal points of any standard lens.

  Application Note

Understanding Focal Length and Field of View

Learn More

Related Product Category: Optical Lenses

View All Now
Was this content useful to you?