
Half Beam Diameter, $ \omega \! \left( z \right) \left[ \text{mm} \right] $: --
Radius of Curvature, $ R \! \left( z \right) \left[ \text{mm} \right] $: --
Rayleigh Range, $ Z_R \left[ \text{mm} \right] $: --
Rayleigh Half Diameter, $ \omega_R \left[ \text{mm} \right] $: --
Half Angle Divergence, $ \theta \left[ \text{mrad} \right] $: --
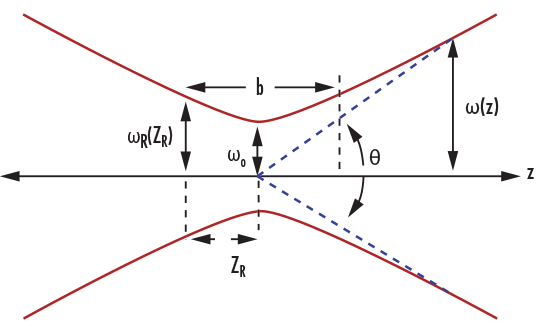
|
$$ z_R = \frac{\pi \omega_0 ^2}{\lambda} $$ |
$$ \omega \! \left( z \right) = \omega_0 \sqrt{1 + \left( \frac{z}{z_R} \right) ^2} $$ |
$$ Z_R = \frac{b}{2} $$ |
|
$$ \omega_R = \omega \! \left( Z_R \right) = \sqrt{2} \cdot \omega_0 $$ |
$$ R \! \left( z \right) = z \left[ 1 + \left( \frac{z_R}{z} \right)^2 \right] $$ |
$$ \theta = \frac{\lambda}{\pi \, \omega_0} $$ |
| $$ \lambda $$ | Wavelength |
| $$ Z_R $$ | Rayleigh Range |
| $$ z $$ | Axial Distance |
| $$ \omega \! \left( z \right) $$ | Half Beam Diameter |
| $$ \omega_0 $$ | Beam Waist |
| $$ b $$ | Confocal Parameter |
| $$ \omega_R $$ | Rayleigh Half Diameter |
| $$ R \! \left( z \right) $$ | Radius of Curvature |
| $$ \theta $$ | Half Angle Divergence |
Mathematically model beam propagation of Gaussian beam using simple geometric parameters. Calculator uses first-order approximations and assumes TEM00 mode to determine beam spot size in free space applications. Please note that results will vary based on beam quality and application conditions.








or view regional numbers
QUOTE TOOL
enter stock numbers to begin
Copyright 2023, Edmund Optics Inc., 18 Woodlands Loop #04-00, Singapore 738100
California Consumer Privacy Act (CCPA): Do Not Sell or Share My Personal Information
California Transparency in Supply Chains Act