Contrast
Authors: Gregory Hollows, Nicholas James
This is Section 2.3 of the Imaging Resource Guide.
Contrast is how well black can be distinguished from white at a given resolution. For an image to appear well defined, black details need to appear black and the white details must appear white (see Figure 1). The more the black and white information trend into the intermediate greys, the lower the contrast at that frequency. The greater the difference in intensity between a light and dark line, the better the contrast. While this may appear obvious, it is critically important.

Figure 1: Transition from black to white is high contrast while intermediate greys indicate lower contrast.
The contrast at a given frequency can be calculated in Equation 1, where Imax is the maximum intensity (usually in pixel greyscale values, if a camera is being used) and Imin is the minimum intensity:
The lens, sensor, and illumination all play key roles in determining the resulting image contrast. Each one can detract from the overall system contrast at a given resolution if not applied correctly and concertedly.
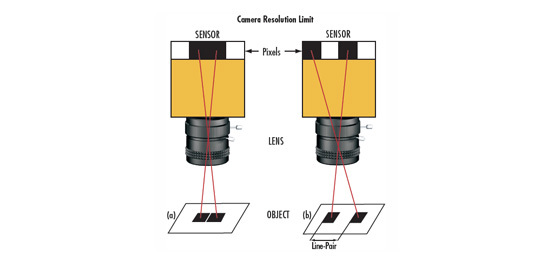
Contrast Limitations for Lenses
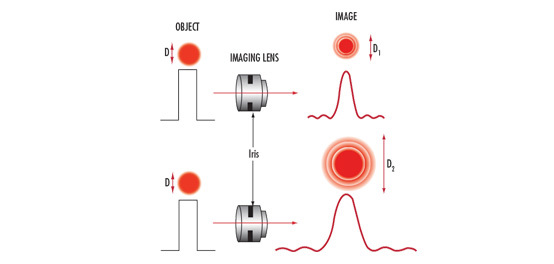
Lens contrast is defined as the percentage of contrast on the object that is reproduced into image space when assuming no contrast loss on the object from illumination. Resolution is meaningless unless defined at a specific contrast. In Resolution, the example assumed perfect reproduction on the object, including sharp transitions at the edge of the object on the pixel. However, this is never the case in practice. Because of the nature of light, even a perfectly designed and manufactured lens cannot fully reproduce an object’s resolution and contrast. For example, as shown in Figure 2, even when the lens is operating at the diffraction limit (described in The Airy Disk and Diffraction Limit), the edges of the dots will be blurred in the image. This is where calculating a system’s resolution by simply counting pixels loses accuracy and can even become completely ineffective.
Consider again the two dots close to each other being imaged through a lens, as in Figure 2. When the spots are far apart (at a low frequency), the dots are distinct, though somewhat blurry at the edges. As they approach each other (representing an increase in resolution), the blurs overlap until the dots can no longer be distinguished separately. The system’s actual resolving power depends on the imaging system’s ability to detect the space between the dots. Even if there are ample pixels between the spots, if the spots blend together due to lack of contrast, they will not easily be resolved as two separate details. Therefore, the resolution of the system depends on many things, including blur caused by diffraction and other optical errors, object detail spacing, and the sensor’s ability to detect contrast at the detail size of interest.














 Previous Section
Previous Section 
















































































































or view regional numbers
QUOTE TOOL
enter stock numbers to begin
Copyright 2024, Edmund Optics Singapore Pte. Ltd, 18 Woodlands Loop #04-00, Singapore 738100
California Consumer Privacy Acts (CCPA): Do Not Sell or Share My Personal Information
California Transparency in Supply Chains Act