The Airy Disk and Diffraction Limit
Authors: Greg Hollows, Nicholas James
This is Section 2.4 of the Imaging Resource Guide.
The Airy Disk
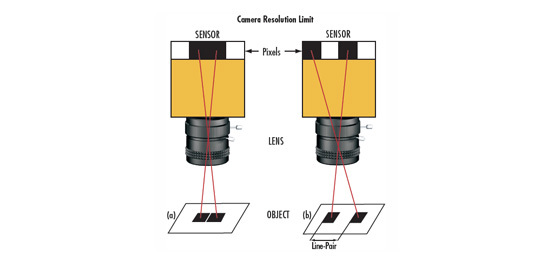
When light passes through any size aperture (every lens has a finite aperture), diffraction occurs. The resulting diffraction pattern, a bright region in the center, together with a series of concentric rings of decreasing intensity around it, is called the Airy disk (see Figure 1). The diameter of this pattern is related to the wavelength (λ) of the illuminating light and the size of the circular aperture, which is important since the Airy disk is the smallest point to which a beam of light can be focused. As focused Airy patterns from different object details approach one another, they begin to overlap (see Contrast). When the overlapping patterns create enough constructive interference to reduce contrast, they eventually become indistinguishable from each other. Figure 1 shows the difference in spot sizes between a lens set at f/2.8 and a lens set at f/8. This effect becomes more of an issue as pixels continue to reduce in size. The Airy disk $ \left( \varnothing_{\small{\text{Airy Disk}}} \right) $, or minimum spot size, can be estimated using the f/# and wavelength (λ):

Figure 1: Diffraction increases as the imaging lens iris is closed (f/# increases). The top lens is set at f/2.8; the bottom lens is at f/8.
Table 1 shows the Airy disk diameter for different f/#s using green light (520nm). The smallest achievable spot size can quickly exceed the size of small pixels. This leads to difficulties in yielding the full resolution capacities of a sensor with any usable level of contrast. Additionally, this does not consider any lens design limitations or manufacturing errors associated with the fabrication of lens elements or the optical assemblies, which can lead to reductions in the ability to produce the smallest physically achievable spot and thus reduce levels of resolution and contrast.
| f/# | Airy Disk Diameter [µm] at a Wavelength of 520nm |
|---|---|
| 2 | 2.54 |
| 2.8 | 3.55 |
| 4 | 5.08 |
| 5.6 | 7.11 |
| 8 | 10.15 |
| 11 | 13.96 |
| 16 | 20.30 |
Table 1: The minimum spot size, or Airy disk, increases with f/# and can quickly surpass pixel size. See Table 1 in Resolution for sample pixel sizes.
Note: This is all theoretical and is the starting point for limitations in an optical system.
The Diffraction Limit
Every lens has an upper-performance limit dictated by the laws of physics and the Airy disk, known as the diffraction limit. This limit is the theoretical maximum resolving power of the lens given in line pairs per millimeter $ \left[ \small{\tfrac{\text{lp}}{\text{mm}}} \right] $. A perfect lens, not limited by design, will still be diffraction limited.
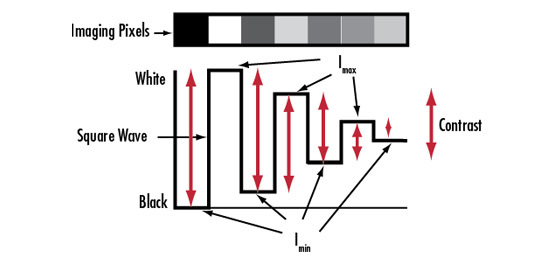
This limit is the point where two Airy patterns are no longer distinguishable from each other (Figure 2 in Contrast). The diffraction-limited resolution, often referred to as the cutoff frequency of a lens, is calculated using the lens f/# and the wavelength of light. Learn more about f/# in f/# (Lens Iris/Aperture Setting).
When the diffraction limit is reached, the lens is incapable of resolving greater frequencies. Table 2 shows the diffraction limit for contrast at 0% at given f/#s. Table 2 shows the diffraction limit for contrast at 0% at given f/#s. These numbers may seem large but are theoretical; several other factors must also be considered. As a rule, and because of inherent background noise, imaging sensors cannot reproduce information at or near 0% contrast. The contrast generally needs to be 10% or greater to be detected on standard imaging sensors. To avoid imaging complications, it is recommended to target 20% contrast or higher at the application-specific critical resolution. Additionally, lens aberrations and variations associated with manufacturing tolerances also reduce performance.
| f/# | 0% Contrast Limit $ \bf{ \left[ \small{\tfrac{\text{lp}}{\text{mm}}} \right]} $ @ 0.520µm |
|---|---|
| 1.4 | 1374 |
| 2 | 962 |
| 2.8 | 687 |
| 4 | 481 |
| 5.6 | 343 |
| 8 | 240 |
| 11 | 175 |
| 16 | 120 |













 Previous Section
Previous Section 















































































































































































or view regional numbers
QUOTE TOOL
enter stock numbers to begin
Copyright 2024, Edmund Optics Singapore Pte. Ltd, 18 Woodlands Loop #04-00, Singapore 738100
California Consumer Privacy Acts (CCPA): Do Not Sell or Share My Personal Information
California Transparency in Supply Chains Act