Dispersion
This is Section 8.8 of the Laser Optics Resource Guide.
Dispersion is the dependence of light’s phase velocity or phase delay as it transmits through an optical medium on another parameter, such as optical frequency, or wavelength. Several different types of dispersion can occur inside an optic’s substrate: chromatic (Figure 1), intermodal, and polarization mode dispersion.1
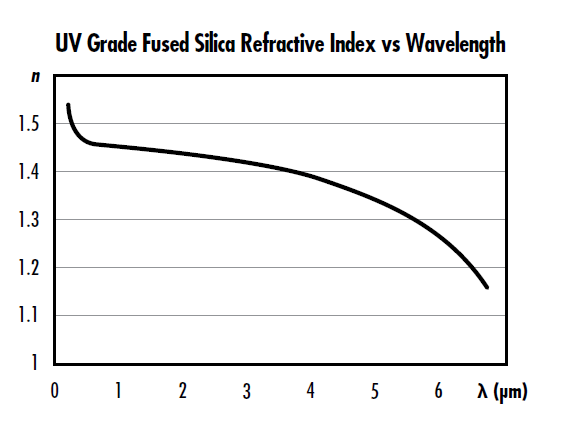
Figure 1: Refractive index of UV Grade fused silica as a function of wavelength
Chromatic Dispersion
The refractive index is the ratio between the speed of light in vacuum and a light wave’s phase velocity while traveling through a medium, such as air or glass. In pulsed laser applications, light is commonly described using frequency because time is generally more critical and the frequency of light is a fixed value, while its wavelength is dependent on the refractive index it is traveling within. Wavelength $ \small{\left( \lambda \right)} $ is related to angular frequency $ \small{\left( \omega \right)} $, refractive index $ \small{\left( n \right)} $, and the speed of light $ \small{\left( c \right)} $ by:
The refractive index of a material is often described using the Selmeier formula and the material constants $\small{B_1}$, $\small{B_2}$, $\small{B_3}$, $\small{C_1}$, $\small{C_2}$, and $\small{C_3}$:
Chromatic dispersion is a dependence of light’s phase velocity $\small{\nu _{p}}$ in a medium on its wavelength, resulting mostly from the interaction of light with electrons of the medium. Chromatic dispersion is described by the Abbe number (Figure 2), which corresponds to the reciprocal of the first partial derivative of refractive index with respect to $ \small{\lambda} $, and partial dispersion, which corresponds to the second derivative of refractive index with respect to wavelength.
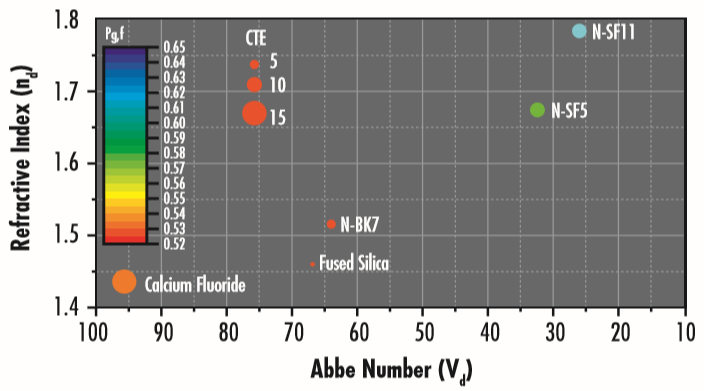
Figure 2: Abbe diagram plot showing the refractive index of common glass types vs their Abbe number. CTE (coefficient of thermal expansion) is defined in the Thermal Properties of Optical Substrates app note.
The Abbe number is given by:
$\small{n_D} $, $\small{n_F} $, and $\small{n_C} $ are the substrate’s refractive indices at the wavelengths of the Fraunhofer D- $ \small{\left( 589.3 \text{nm} \right)} $, F- $ \small{\left( 486.1 \text{nm} \right)} $, and C- $ \small{\left( 656.3 \text{nm} \right)} $ spectral lines. The Abbe number of a material may also be described at any wavelength using the derivative of refractive index with respect to wavelength:
In laser applications, the primary concern is how dispersion will affect the properties of a laser pulse traveling through the medium, which is described by group velocity - the variation of the phase velocity of light in a medium relative to its wavenumber:
The wavenumber $ \small{\left( k \right)} $ is $ \tfrac{2 \pi}{\lambda} $ - this concept is sometimes also referred to a spectral phase. As multiple wavelengths of light transmit through a material, the longer wavelength (lower frequency) typically travels faster than shorter wavelengths (higher frequencies) because the group velocity is wavelength-dependent.2 This results in a spectral spreading of the wavefront phase similar to the way light transmitting through a prism is dispersed into its component colors. Group velocity is defined as the first derivative of the phase velocity with respect to frequency, and the group velocity dispersion $ \small{\text{GVD}} $ is similarly defined as the derivative of the inverse group velocity with respect to frequency:
Group velocity is similar to spectral dispersion as they both correspond to the first derivative of refractive index with respect to wavelength or frequency. Likewise, $ \small{\text{GVD}} $ is similar to partial dispersion in that they are both second derivatives with respect to wavelength or frequency. Minimizing $ \small{\text{GVD}} $ in an optical design is similar to designing to minimize chromatic focal shift, except the designer will focus on group velocity and $ \small{\text{GVD}} $ rather than the Abbe number and partial dispersion.
A further discussion of $ \small{\text{GVD}} $ and its importance for ultrafast laser optics can be found in our Ultrafast Dispersion application note.
Intermodal Dispersion
Intermodal dispersion is a dependence of the group velocity of light in a waveguide, such as a multimode fiber, on the optical frequency and the propagation mode.2 In multimode optical fiber communication systems, this severely limits the achievable data transmission rate, or bit rate. Intermodal dispersion could be prevented by using single-mode fibers or multimode fibers with a parabolic refractive index profile.
Polarization Mode Dispersion
Polarization mode dispersion is the dependence of light’s propagation characteristics in a medium on polarization state, which can be relevant in high data rate single-mode fiber systems. All three types of dispersion may cause temporal broadening or compression of ultrashort pulses in free space or optical fibers, potentially causing separate pulses blend together and become unrecognizable (Figure 3).
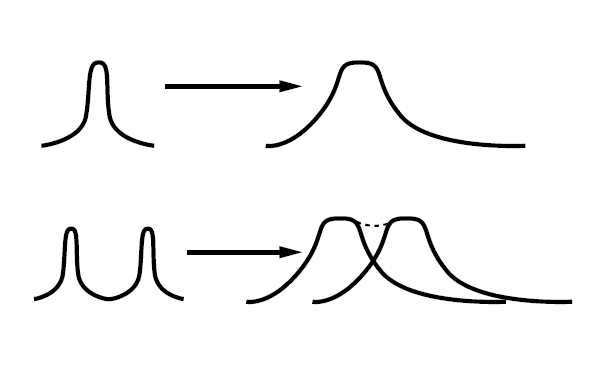
Figure 3: Dispersion can cause laser pulses traveling down fibers to spread until they become unrecognizable
References
1 Paschotta, Rüdiger. Encyclopedia of Laser Physics and Technology, RP Photonics, October 2017, www.rp-photonics.com/encyclopedia.html.
2 Ghatak, Ajoy, and K. Thyagarajan. “Optical Waveguides and Fibers.” University of Connecticut, 2000.
More Resources
- Ultrafast Dispersion
- Wavelength Effects on Performance
- Chromatic and Monochromatic Optical Aberrations
- Why Use an Achromatic Lens?
- "An achromat singlet" by Joel Bagwell, Christian Hebert, and Nathan Carlie - SPIE
- Absorption
- Optical Glass
- Thermal Properties of Optical Substrates
- Homogeneity and Scatter from Inclusions and Bubbles
- Subsurface Damage
- Common Laser Optics Materials
- Laser Optics Lab Video Series













 Previous Section
Previous Section 

























































or view regional numbers
QUOTE TOOL
enter stock numbers to begin
Copyright 2024, Edmund Optics Singapore Pte. Ltd, 18 Woodlands Loop #04-00, Singapore 738100
California Consumer Privacy Acts (CCPA): Do Not Sell or Share My Personal Information
California Transparency in Supply Chains Act