Wavelength Effects on Performance
Authors: Gregory Hollows, Nicholas James
This is Section 3.3 of the Imaging Resource Guide
Different wavelengths bend at different angles as light passes through a medium (glass, water, air, etc.). This is commonly observed when sunlight passes through a prism and creates a rainbow effect; shorter wavelengths are bent more than longer ones. This same effect creates problems when trying to resolve details and gain information in imaging systems. To avoid this issue, imaging and machine vision systems commonly use monochromatic illumination, which involves only single wavelengths or narrow bands of the spectrum. Monochromatic illumination, e.g. from a 660nm LED, practically eliminates what are known as chromatic aberrations in an imaging system.
Chromatic Aberrations

Figure 1: Lateral Color Shift
Chromatic aberrations exist in two fundamental forms: lateral color shift (Figure 1) and chromatic focal shift (Figure 2).
Lateral color shift, Figure 1, can be seen as you move from the center of the image towards the edge of the image. In the center, the spots for different wavelengths of light are concentric. Moving towards the corner of the image, wavelengths tend to separate and produce a rainbow effect. As a result of this color separation, a given point on the object is imaged over a larger area, resulting in reduced contrast. On sensors with smaller pixels, this result is even more pronounced, as the blurring spreads over more pixels. In depth details on lateral color can be found in How Aberrations Affect Machine Vision Lenses.
Chromatic focal shift, Figure 2, relates to the ability of a lens to focus all wavelengths at the same distance away from the lens. Different wavelengths will have different planes of best focus. This shift in focus with respect to wavelength results in reduced contrast, since the different wavelengths create different size spots at the image plane where the camera sensor is located. In the image plane of Figure 3.7 a small spot size in the red wavelengths, a larger spot size in green, and the largest spot size in blue is shown. Not all colors will be in focus all at once. Advanced details can be found in How Aberrations Affect Machine Vision Lenses.

Figure 2: Chromatic Focal Shift
Choosing the Optimal Wavelength
Monochromatic illumination enhances contrast by eliminating both chromatic focal shift and lateral chromatic aberration. It is readily available in the form of LED illumination, lasers, and through the use of filters. However, different wavelengths can have different MTF effects in a system. The diffraction limit defines the smallest theoretical spot which can be created by a perfect lens, as defined by the Airy Disk diameter, which has a wavelength (λ) dependence. See Limitations on Resolution and Contrast: The Airy Disk, for more details on the Airy Disk and diffraction limit. Using the Equation 1, one can analyze the change in spot size for both different wavelengths and different f/#s.
Table 1 features the calculated Airy disk diameter for wavelengths ranging from Violet (405nm) to Near-Infrared (880nm) at various f/#s. This data clearly shows that lens systems have better theoretical resolution and performance when they are utilized with shorter wavelengths. The benefits to understanding this are multi-fold. First, shorter wavelengths allow for better utilization of the sensor’s pixels regardless of size due to the smaller achievable spot size. This is especially pronounced on sensors with very small pixels. Second, it allows for more flexibility to use higher f/#s, which will allow for greater depth of field. For example, a red LED could be used at f/2.8 to generate a spot size of 4.51μm or a blue LED could be used to generate almost the same spot size at f/4. If both options yield acceptable levels of performance at best focus, the system set at f/4 using blue light will produce better depth of field, which could be a critical requirement. Advanced details may be found in Sensor Relative Illumination, Roll Off and Vignetting
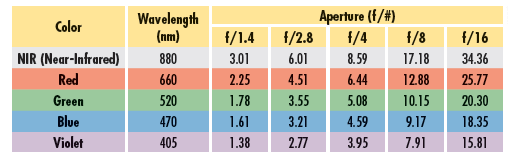
Table 1: Theoretical Airy Disk Diameter Spot Size (in μm) for various Wavelengths and f/#s
Example 1: Improvement with Wavelength
Both images in Figure 3 are taken with the same lenses and camera producing the same field of view, thus presenting the same spatial resolution on the object in lp/mm. The camera utilizes 3.45μm pixels. The illumination used in Figure 3a is set at 660nm and 3b at 470nm. The high resolution lens was set to higher f/# to greatly reduce any aberrational effects. This allows diffraction to be the primary limitation in the system. The blue circles are representative of the limiting resolution at in Figure 3a. Note that Figure 3b has a significant increase in resolvable detail (approximately 50% finer detail). Even at the lower frequencies (wider lines), there is a higher level of contrast with 470nm illumination in Figure 3b.


Figure 3: Images of a Star Target taken with the same Lens, at the same f/#, with the same Sensor. The Wavelength is varied from 660nm (a) to 470nm (b)
Example 2: White Light vs. Monochromatic MTF
In Figure 4, the same lens is used at the same working distance and f/#. Figure 4a is using white light, and Figure 4b is using 470nm illumination. In Figure 4a, all of the performance is at 50% or below at the Nyquist limit. For Figure 4b, all of the performance at the Nyquist limit is higher than Figure 4a. Additionally, performance in the center of the system in Figure 4b is above the diffraction limit of Figure 4a. The reason for this increase in performance is twofold: using monochromatic light eliminates chromatic aberrations in the system which generally allows for much smaller spots to be created, and 470nm illumination is one of the shortest wavelengths of light that is used in visible range imaging. As detailed in the sections on diffraction limit and Airy Disk, shorter wavelengths allow for higher levels of resolution.
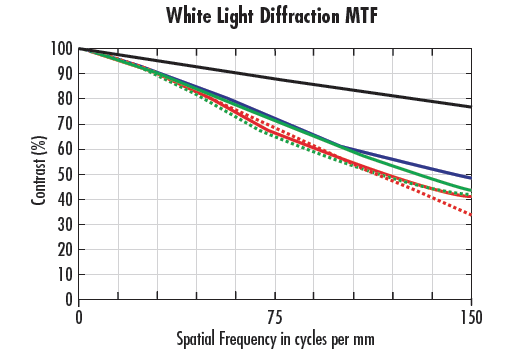
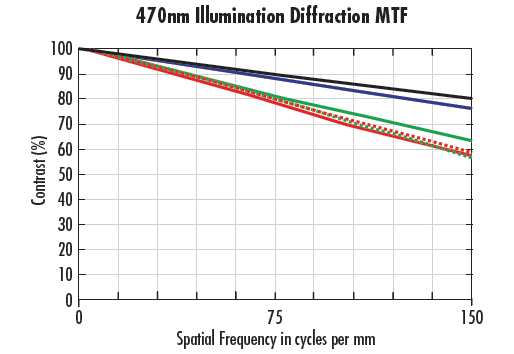
Figure 4: MTF Curves for the same Lens at f/2 using a different Wavelengths; White Light (a) and 470nm (b)
Wavelength Considerations
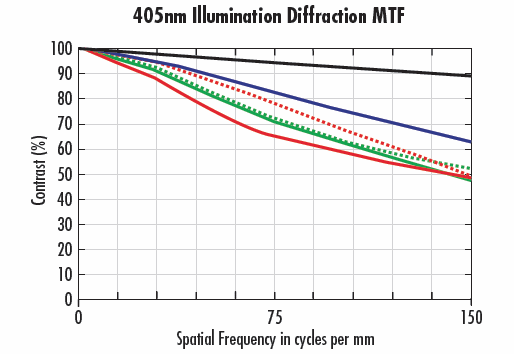
A few issues can arise with changing wavelength that need to be understood. From a lens design perspective, the further into the blue portion of the spectrum, as wavelengths become shorter, the more a lens design can struggle regardless of how narrow the waveband that is used. Essentially, glass materials tend to not perform well at shorter wavelengths. Designs do exist in this region of the spectrum, but they are often limited in their capabilities, and the exotic materials that may be required to build the lens can be costly. The best theoretical performance seen in Table 1 is at the violet wavelength of 405nm, but most system designs cannot perform well in this area. It’s very important to evaluate what a lens can realistically do at such short wavelengths using lens performance curves.
Example 3: Theoretical Limitations
Figure 5 compares a 35mm lens at f/2 with blue (470nm) and violet (405nm) wavelengths (5a and 5b respectively). While Figure 5a has a lower diffraction limit, it also shows that the 470nm wavelength yields higher performance at all field positions. The effect here is increased when the lens is used at the extremes of its design capabilities for f/# and WD (detailed in Modulation Transfer Function (MTF) and MTF curves).
Another wavelength issue that can greatly affect performance is related to chromatic focal shift. As the application’s wavelength range increases, the lens’s ability to maintain high levels of performance will be compromised. How Aberrations Affect Machine Vision Lenses goes into more detail on the phenomenon.













 Previous Section
Previous Section 



























































































or view regional numbers
QUOTE TOOL
enter stock numbers to begin
Copyright 2024, Edmund Optics Singapore Pte. Ltd, 18 Woodlands Loop #04-00, Singapore 738100
California Consumer Privacy Acts (CCPA): Do Not Sell or Share My Personal Information
California Transparency in Supply Chains Act